Learning Assembly — Part 4.1
Let’s Write Some Assembly Language Code!
By looking at some simple examples, we can learn how to write Assembly Language code.
Assembly is a very low-level programming language - everything you write is “close to the metal”. What this means is that the language is very related to the hardware it is on. In this article, we will learn how to write a variant of Assembly language. Specifically, we will be looking at 6502 Assembly Language. The 6502 is a classic processor, found in lots of old tech. Don’t let age worry you though, the core tenets of Assembly will be the same whether we are looking at a 6502 or and intel i7.
To learn how to write this code we will take a look at two small examples. The examples have been picked to give us a brief idea of the basic features of the language. We will also look at how we can make our code more readable by using features that the Assembler can provide us.
Technically, this is Part 4 of a “learning assembly” series I am writing. However, wherever possible I am trying to ensure each part is independent. If all you’re interested in is getting the basics of assembly, hopefully, this will be suitable for you as well.
Let’s begin with a very brief recap of the 6502 hardware.
A Small Recap
An Assembly Language could be defined by its instruction set. An instruction is a command that the processor will be able to interpret (like add, or to move something around in memory). The instructions available to us are deeply linked to the hardware itself. Using a 6502 processor gives us access to around 50 instructions. Outside of these 50 instructions, if we want the processor to do something, we will need to create it ourselves.
A deeper dive into the 6502 hardware is available here, but we can go over some things that may be important for us today:
The Accumulator: This is the part of the 6502 hardware that can help us do arithmetic. If we wanted to add two numbers, we could send them into the accumulator, where they would “accumulate” together.
The Carry Register: Imagine if we did the sum 26 + 15.
(1) <- our carry
26
+̲ ̲1̲5̲
41Well, we’ve added 5 and 6, which gives 1, carry-a-1. Then we could do 20 + 10 + the-10-we’ve-carried-over to give 40. Combining these we get the answer of 41.
Well, when we add binary numbers something similar happens — we still carry things. However, in 6502 we can only keep track of things that fit in an 8-bit number. If we do some maths that results in us carrying something that won’t fit into 8-bits, we need to keep track of this. For example 1000 0001 + 1000 0000 gives 1 0000 0001. However, we cannot fit the left-most 1 we had to carry into 8-bits, but, we also cannot forget about it if we want our maths to work.
This concept of carrying a number if it falls out of 8-bits is handled by the 6502 hardware in the Carry register. It’s just something we’ll try to keep in mind when we do maths.
Addition
Our easiest example will be 1 + 2. Here's some code:
LDA #01
ADC #02
STA $0402On the left of each line is the instruction while on the right is the data or memory location needed to make the instruction work. This style is how Assembly language is written. Let’s go through the example one line at a time.
Line 1: LDA is telling the 6502 to load the piece of data that follows into the Accumulator (A). Here, it is #01. We can prefix our data with a symbol to tell the assembler what sort of data we are passing it. In this case, we are using a hashtag which means our data is a 'literal' - we are literally passing it a number. After this line, the contents of A is 1.
Line 2: ADC means to add the following value onto whatever is currently in the Accumulator. The 'C' in the instruction tells us it will be keeping track of any carrys that have happened in previous calculations. Here, we assume C = 0. Therefore, all we are adding to the Accumulator is#02. Now, the value in A is 3.
Line 3: The STA instruction will send the contents of the Accumulator to a location in memory. In our example, this will send the value 3 to the memory address $0402. Note, we have not used a # - this is because it is not literal, it is an address. Furthermore, we have used $ which tells the assembler this value is in binary.
After these three instructions, we have successfully done 1 + 2 — well done! If we wanted to view the answer we would have to look in $0402.
Addressing and Flags
In Part 3, we discussed the numerous registers that could be set in the 6502. These have numerous uses, among them is to keep track of aspects of arithmetic. We also mentioned, above, that ADC will also add anything that has been carried from the last calculation (ie, anything in the carry register). We need to be careful that what is happening is actually what we want to happen. We don’t want to be adding in the Carry when we don’t want to and we don’t want to miss it out if we actually want it. We can manually clear the flags to ensure no unexpected values are involved in our arithmetic - better safe than sorry. This is what CLC (clear carry flag) and CLD (clear decimal flag) do.
In the previous example, we referred to the values 1 and 2 directly. There, it was ok as we only have a small number of values we need to use in our calculation. However, if we were doing something more involved this would get tiring. In Python, you can call a variable ‘x’ or ‘y’ and use them throughout your code. What is common to do in is to store your values somewhere in memory, then in your code point to that memory location. This will save us explicitly passing values around. For example, the value 1 might be stored in the location $0400 and the value 2 in $0401. Now, we can just refer to them and get the same result as before.
Below is some code with these two changes made.
CLC
CLD
LDA $0400
ADC $0401
STA $0402As well as built-in features of the assembly language, functionality can come from the assembler you choose. Here are some useful features available in most assemblers:
- You can store values in a "variable". So, you could say
ADR1 = $0400and then whenever you calledADR1the assembler would understand you meant the address contained within it. - You can leave comments with ";".
- You can "name" blocks of code. This allows us to refer to it numerous times in our program. We will see an example soon where this can be useful.
The code below incorporates the above suggestions:
ADR1 = $0400
ADR2 = $0401
ADR3 = $0402
CLC ; clear carry bit
CLD ; clear decimal bit
ADD LDA ADR1 ; load the contents of ADR1 into accumulator
ADC ADR2 ; add the contents of ADR2 to accumulator
STA ADR3 ; save result to ADR3Now, our simple code uses more features of the language and assemblers. It is hopefully easier to read and will be easier for us to use and build upon.
In the future, we will look at how to get this running on your machine. But for now, I think it’s interesting in itself to see how something as simple as addition can be broken down into much smaller pieces.
A Small Division Cheat
Before attempting multiplication (next time!) we will have a quick look at dividing by 2. This can be done easily by looking at operations we can perform on binary numbers. Let’s look at what happens if we shift a binary number to the right. The number 16 (0001 0000) becomes 8 (0000 1000) and 56 (0011 1000) becomes 28 (0001 1100). Shifting them to the right is the equivalent of dividing by two! Compared to doing "proper" division and multiplication it is significantly easier. It’s also quite cool, I think!
This sort of shifting is made possible by numerous instructions the 6502 has. The instruction set contains 2 shifts and 2 rotates. The following figure shows an example of each:
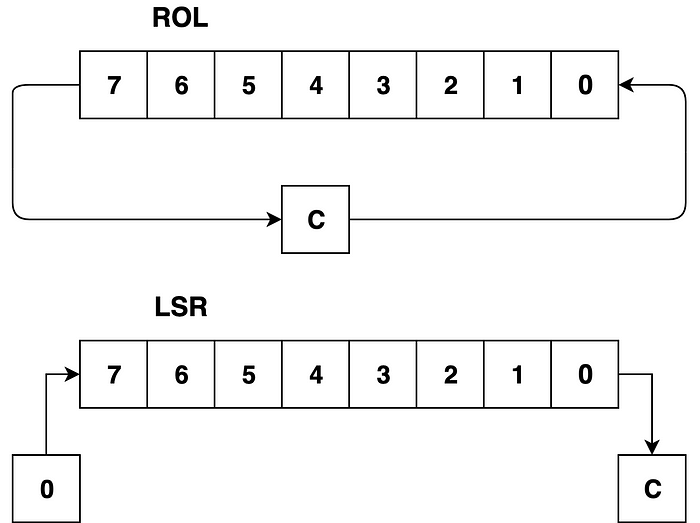
ROL rotates the number to the left, with the left-most bit falling into the carry register while the old contents of C move into the right-most bit.
LSR shifts the number to the right. Here though, the right-most bit falls into the carry, but the left-most is replaced by 0. This is what we can use to divide by two.
These two instructions have equivalents that go in the opposite direction as well. For the meantime, however, ROL and LSR will be necessary for us to do multiplication.
Here is a short example of what division might look like:
ADR1 = $0400
CLC ; clear carry bit
CLD ; clear decimal bit
DIV LSR ADR1 ; shift all the bits in ADR1 to the rightConclusion
We have seen two useful examples of code: addition and a simplified version of division. These examples begin to expose us to the range of instructions that are available on the 6502.
This article used to have around a 20-minute read length but I decided to split it in two for the sake of readability. So, next time, we will be looking at a more complex example: multiplication.
This is the fourth part of my “learning assembly” series.
- Part 1: Introduction to 6502 Assembly
- Part 2: Get to Grips with Binary Numbers
- Part 3: How do Processors work?
- Part 4.1: Let’s Write Some Assembly!
- Part 4.2: Let’s Write Some (Harder) Assembly!
- Part 5: The Apple ii
This article has been adapted from my personal blog. Most of the content I talk about will come from two main sources: “6502 Assembly Language Programming” by Lance A.Leventhal and “Programming the 6502” by Rodney Zaks.